『正規形』はデータベース理論の中でももっとも重要な項目です。更新異常・矛盾の起こらないデータベースを構築するため、正規形の理論は必ず理解しましょう。関係スキーマ/テーブルを正規形に変形することを『正規化』といいます。
非正規形と第一正規形
まず、単純な例で考えてみます。
以下は、今学期の科目履修状況についての説明文です。
鈴木君は、『データベース演習』と『MOS対策』を履修した。
佐藤君は、『データベース演習』と『MOS対策』を履修した。
田中君は、『MOS対策』と『Webデザイン概論』を履修した。
高橋君は、『データベース演習』と『Webデザイン概論』を履修した。
この内容を表にすると、以下のようになります。

人間が見るならばこれでも問題はないのですが、データベースとしてはデータが使いにくいのです。
この表では、『鈴木君の履修している科目は?』という情報は簡単に検索できるのですが、『データベース演習を履修している学生は?』という情報を簡単には探せません。
論理設計の段階からは逸脱しますが、SQLをよく勉強した人は
『LIKE演算子をつかえばいいのでは?』
と思いつくかもしれません。
たしかに、
WHERE 科目 LIKE '%データベース演習%'とすれば『科目名』に『データベース演習』を含むレコードを抽出することができます。
しかし、もし田中君が似た科目名の『データベース演習II』という科目を履修していたらどうなるでしょう?
WHERE 科目 LIKE '%データベース演習%'は、『データベース演習』だけでなく『データベース演習II』という文字列でも条件が成立してしまうため、『データベース演習』を履修していない田中君まで抽出されてしまいます。
実はこの問題は、関係スキーマ/テーブルの構造以外に属性(項目)の中の書式まであらかじめ決めておかなければSQLでは解決できないのです。
しかし、このような『属性(項目)の中の書式』に依存したデータ構造は、データの再利用性を損なってしまうため、できるだけ避けるのが良い設計です。
というわけで、ここで1つ、関係スキーマ/テーブルを設計する際に守るべき条件を設定します。
『属性(項目)の中に、書式(構造)をもちこまない』
つまり、
『1つの属性の中には、<単純な>=<それ以上分解できない>値だけしか挿入しない』
ということです。
データベース用語で簡潔に表現すると、
『すべての属性が、単純属性である』
となります。
関係スキーマやテーブルについて、この条件を満たしたものを、『第一正規形』といいます。
第一正規形の条件を満たしていないものを『非正規形』といいます。
【科目履修状況】を第一正規形として表にすると以下のようになります。
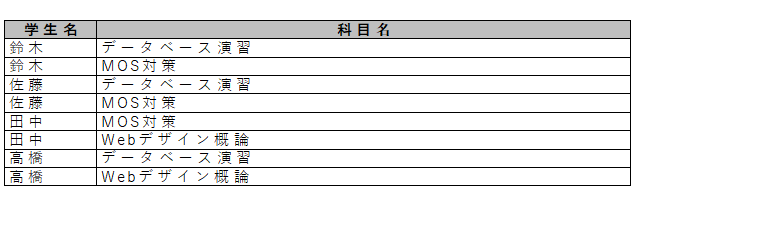
行数が増えてかえってごちゃごちゃしたように感じるかもしれませんが、データの検索はこちらの方が単純に済みます。『データベース概論を履修している学生』を知りたい場合には、単純に『科目=”データベース概論”である行』を探すだけで済みます。『データベース概論II』という紛らわしい名前の科目を履修している学生がいても間違って抽出されることはありません。
単純属性の例外
『単純属性』は言葉の定義としては『それ以上分解できない属性』です。
しかし、分解可能な情報でも、単純属性に準ずるものとして扱う場合もあります。
例えば、
『日付(年月日)』は『年』と『月』と『日』に分割できる
『電話番号』は『市外局番』と『市内局番』と『市内番号』に分解できる
『学籍番号』はケタ毎に『入学年度』と『学部・専攻』と『学部・専攻内での番号』に分解できる
と、それぞれ分解可能な情報です。
しかしたとえば
『市外局番とは無関係に、市内局番が3812の人だけ抽出したい』とか、
『学籍番号の2桁目が4の人だけ抽出したい』という需要があるでしょうか?
分解した各項目を別々に扱うことがなく、全体で1つの値とみなすことが多い場合には、それ以上分解する必要はないでしょう。
もしかしたら『5月生まれの人を抽出したい』という需要ならあるかもしれません。そういう場合は『日付』をさらに『年』『月』『日』に分解して設計するのもよいでしょう(実在のデータベースの多くは日付を1つの値として格納し、必要に応じて年月日に分解して取り出す機能があるので、『年』『月』『日』をそれぞれ別の属性として設計することはまずありません)。
導出可能属性
導出可能属性(他の属性の値から計算などによって一意に導き出すことができる項目、例えば単価×個数で合計金額が判る、など)も単純ではない属性として第一正規形で排除すべき、とする場合もあります。
候補キー、主キー
もう少し複雑な例を考えてみます。先ほどの表に、学籍番号と科目IDを追加します。
当然、
学籍番号がわかれば学生名は決定できる
科目IDがわかれば、科目名は決定できる
とします。
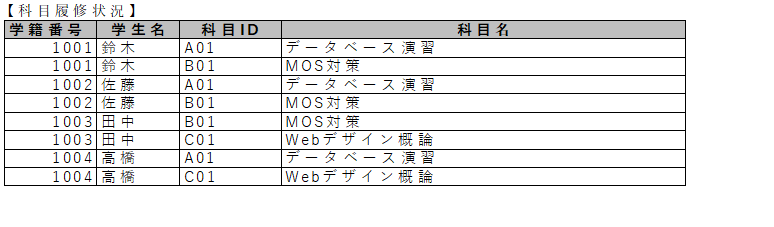
この表の候補キーを考えてみましょう。
候補キーとは、『タプルを一意に特定できる、最小限の属性の組』です。この表の場合は、{学籍番号、科目番号}となります。候補キーが1つしかないので、自動的にこれが主キーとなります。
よって、この例を関係スキーマとして記述すると
科目履修状況(学籍番号、学生名、科目ID、科目名)
となります。
その他の非正規形の問題点
非正規形の表にも学籍番号と科目IDを追加してみます。

先ほど挙げた単純属性ではないことによる問題の他、この形式では『データベース演習の科目IDがA01である』という情報が確実には読み取れない、という問題があります。
練習問題1
次の例を、第一正規形の表にしなさい。
(1)
10/3の売上は、200円のバナナが1房と、100円のリンゴが2個だった。
(2)
『秀吉』と『南殿』の間には、『秀勝』という息子がいる。
練習問題2
次の表を第一正規形にしなさい。
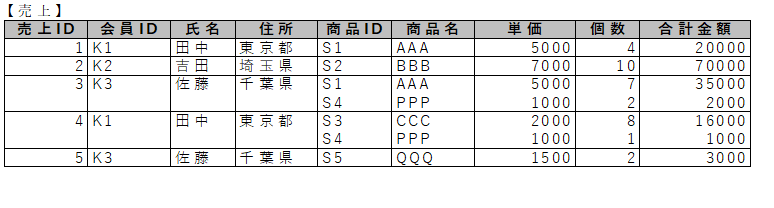


コメント