第2正規形
部分関数従属と完全関数従属
先ほどの【科目履修状況】をもう一度見てみましょう。

テーブルの構造を表すと、
科目履修状況(学籍番号、学生名、科目ID、科目名)
でした。この表の候補キーは(学籍番号、科目ID)です。
つまり、すべての属性は(学籍番号、科目ID)に関数従属してます。
しかしよく見ると、
『学生名』は『学籍番号』だけでも決定できる
『科目名』は『科目ID』だけでも決定できる
というように、候補キーの属性がすべて揃わなくても値が決定できる属性があります。
このように、
『属性の組Xの一部の属性の値だけでも、属性(または属性の組)Yの値が定まる』
ことを、
YはXに部分関数従属している
といいます。
反対に、『属性の組Xのすべての属性が判らないと、属性(または属性の組)Yの値が定まらない』ことを、
YはXに完全関数従属している
といいます。
第2正規形
ここで新たに、テーブルの設計のための条件を設定します。
『候補キーの一部分だけで判ってしまう属性がない』
データベース用語で簡潔に表現すると、
『すべての非キー属性が、候補キーに完全関数従属している』
となります。
第一正規形の条件を満たし、かつ、この新しい条件も満たしたテーブルを、『第二正規形』といいます。
テーブルの分割
では、どのように操作すれば第二正規形になるでしょうか。
すべての非キー属性が候補キーに対して完全関数従属するようにしたいのですから、候補キーに対して部分関数従属する非キー属性を別の表に分けてしまうことにします。
ここでは話を簡単にするため、候補キーではなく主キーのみについて考えてみます。
先ほどの例の
科目履修状況(学籍番号、学生名、科目ID、科目名)
の主キーは(学籍番号、科目ID)なので、
このテーブルには『学籍番号と科目IDの両方が判らなければ決定できない属性』のみを残し、
『学籍番号』および『学籍番号だけで決定できる属性』
『科目ID』および『科目IDだけで決定できる属性』
をそれぞれ別の表に移すことにします。
具体的には、まず
学籍番号 → 学生名
という関数従属がありますから、『学籍番号』と『学生名』のテーブルを作ります。名前は『学生』とでもしましょう。主キーは、もとの主キーを引き継いで『学籍番号』にします。
これで1つ、新しい関係スキーマ/テーブルができました。
学生(学籍番号、学生名)

もちろん表から重複は省きます。
次に、
科目ID → 科目名
という関数従属がありますから、『科目ID』と『科目名』のテーブルを作ります。名前は『科目一覧』とでもしましょう。主キーは、もとの主キーを引き継いで『科目ID』にします。
これでもう1つ、新しい関係スキーマ/テーブルができました。
科目(科目ID、科目名)

最後に、もとのテーブルからは、主キーに部分関数従属していた非キー属性を削除します。この例の場合、主キーに完全関数従属していた非キー属性は存在しませんので、主キーだけが残ります。
よって、【科目履修状況】はこうなります。
科目履修状況(学籍番号、科目ID)

このように、主キーに完全関数従属する非キー属性が存在しない場合でも、もとのテーブルそのものをなくしてしまうことはできません。たとえばこの例の場合、『学籍番号』と『科目ID』だけになった【履修科目状況】がなければ『誰がどの科目を履修しているか』という情報がどこにも残りません。
練習問題3
下の第一正規形の表を、第二正規形にしなさい。
ただし、会員IDが判れば氏名および住所は決定でき、商品IDが判れば商品名と単価が決定できるものとします。
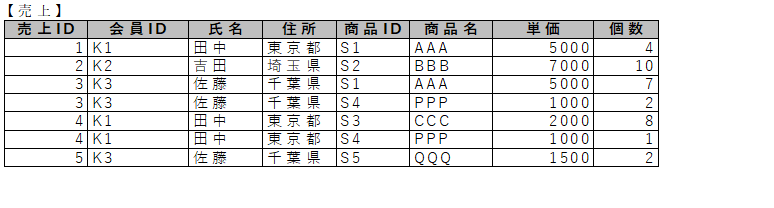
売上(売上ID、会員ID、氏名、住所、商品ID、商品名、単価、個数)



コメント